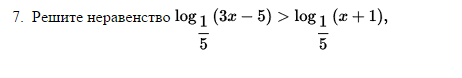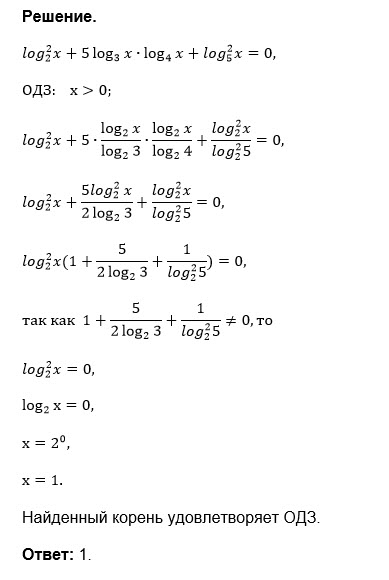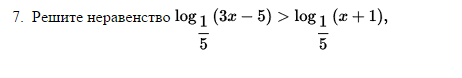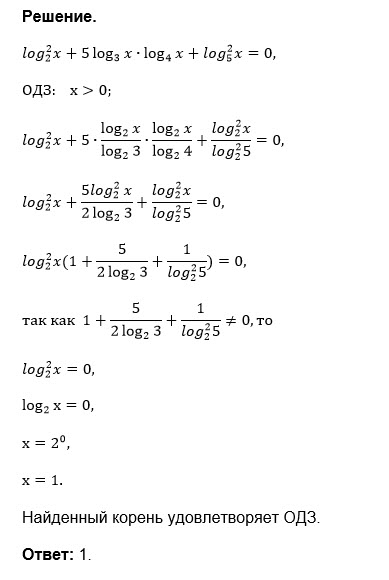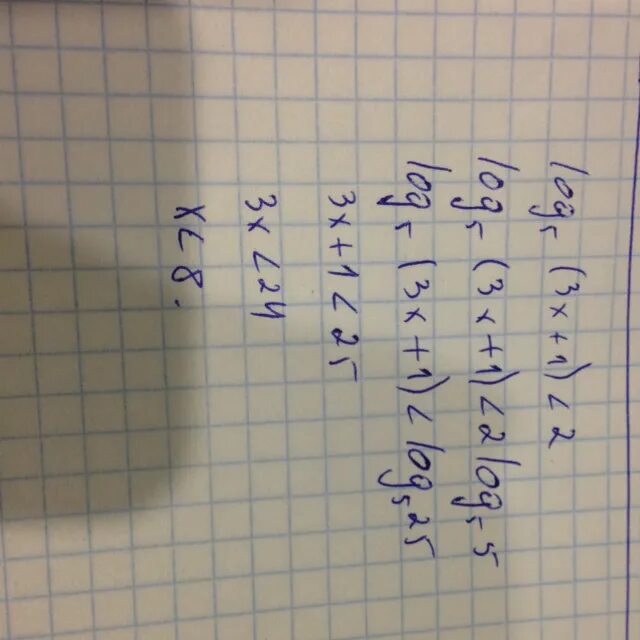Log5(2x+3)>log5(x-1). Log5(3x+1)=2. Решить уравнение log. X3 и x5. Log3 x 5 3.
|
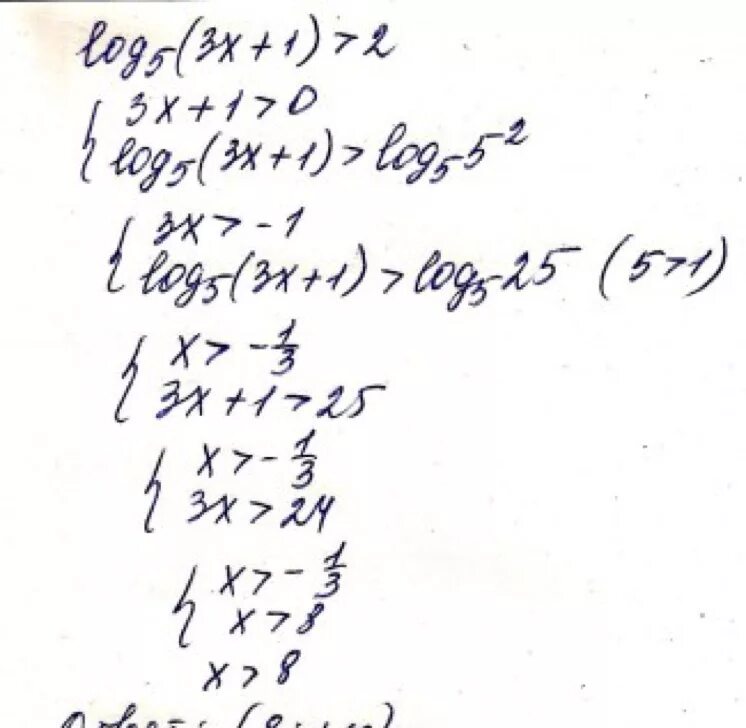Log x^2 одз. 2log5x log корень x x-log1/5x 8. Log0,5(x2+4x-5)=-4. Log3 x 5 3. Найдите корень уравнения log3(2x−5)=2.
|
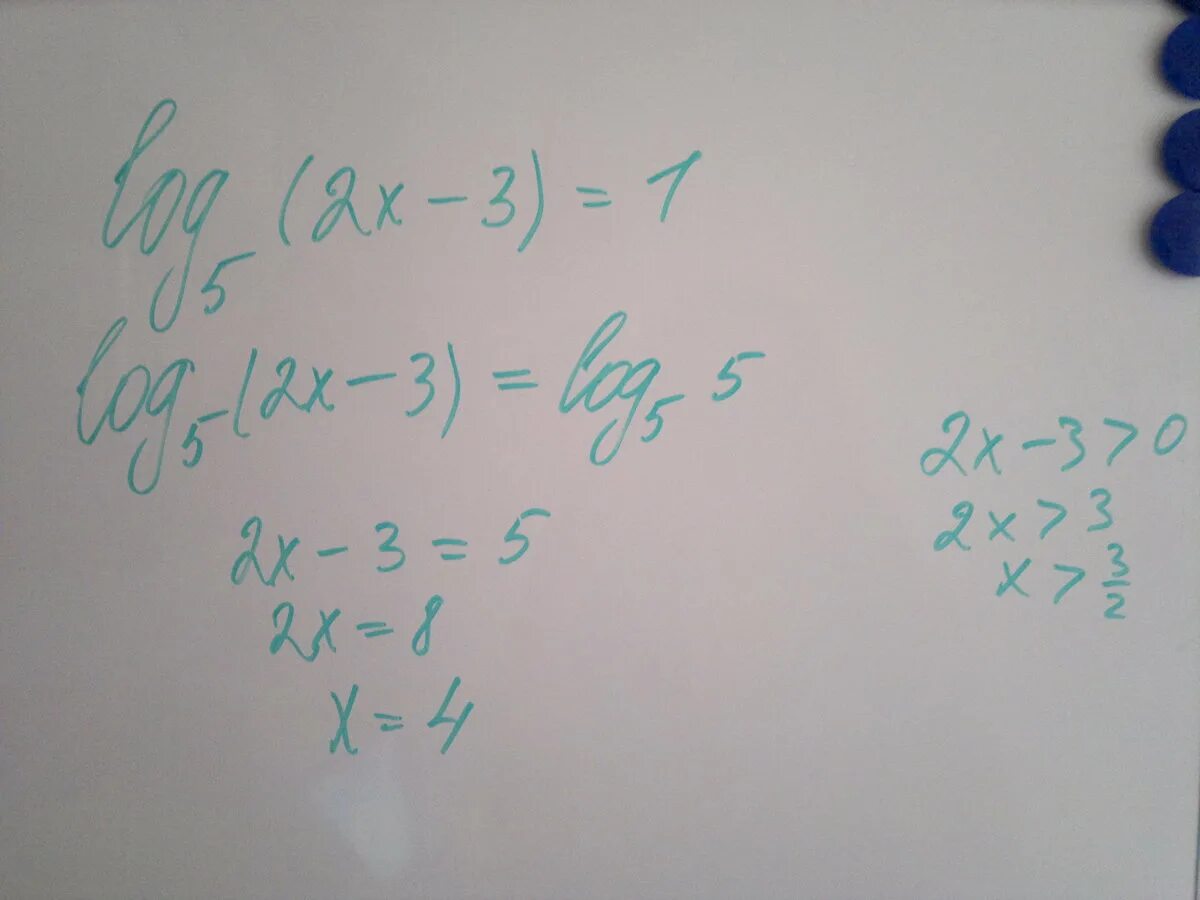Log3 x 5 3. Log5x>1. Log 5 (3х-1)=3. Log0,5(3x-1)=-3. Log3 3.
|
Log 4 (x-2)= 2 уравнения. Решить уравнение log1\2 5x-1==-2. Log2 x 5 log2 x+2 3. Log1 5 3x-5 log1 5 x+1. Log2log 2 x^3+8 log 2 x+2 + 2log2 4-x.
|
X3 и x5. Лог 2 5 - 2. Log3 x 5 3. Log5(3-х)=2. Log(x+1)+log(2x+4/x+1.
|
Log3 x 5 3. Log3 x 5 3. 3log1/2x+5log1/2x-2. Log3 x 5 3. Log2(x+2)=5.
|
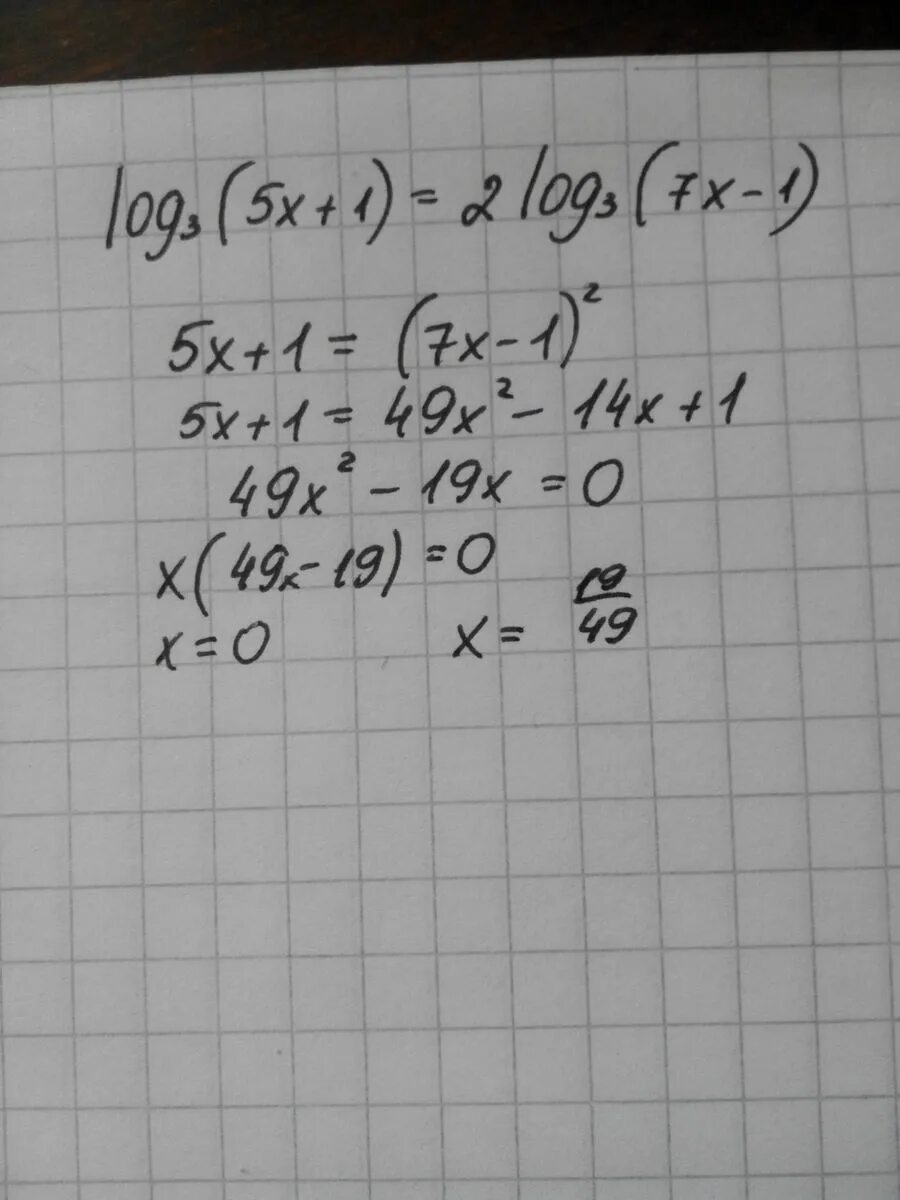Log3 x 5 3. Log5 1/5. Log3 x 5 3. Log по основанию 1/4 (5x-x^2) + корень 5 ^log3 1<0. Log0 2 x 2 4 x-8 x-5 0.
|
Log3 x 5 3. Log5(x-3)<2. Log3 5x 3 log3 7x+5. Log x 1 2x 5 log 2x-5 x+1 2. Log3 2x 5 log3 2x-3 1.
|
Log3 x+log корень 3 +log 1/8 x =6. 9 log 3 4 решение. 9log3 4. Log3 x 5 3. Log0,5 (5+2х)=1.
|
Log3 x 5 3. 3 2 log3 5. Log 1/5(4х+3)-log1/5 4 = log1/5 2. Log5(3-х)=2. Лог 2 х-3 х+5 лог 2 х-3 х+5 2.
|
Log3 x 5 3. Найдите корень уравнения: log (5 - x) = 2. Log3 x 5 3. Лог 3 3. Log2(3x-1)-log2(5x+1)<log2(x-1)-2.
|
Решение уравнения log x (х^3-5х+7) =3. Лог 3 5-х + лог 3-1-x =3. Log3 x 5 3. 5^x-log2(x). Log5(3x+1)=2.
|
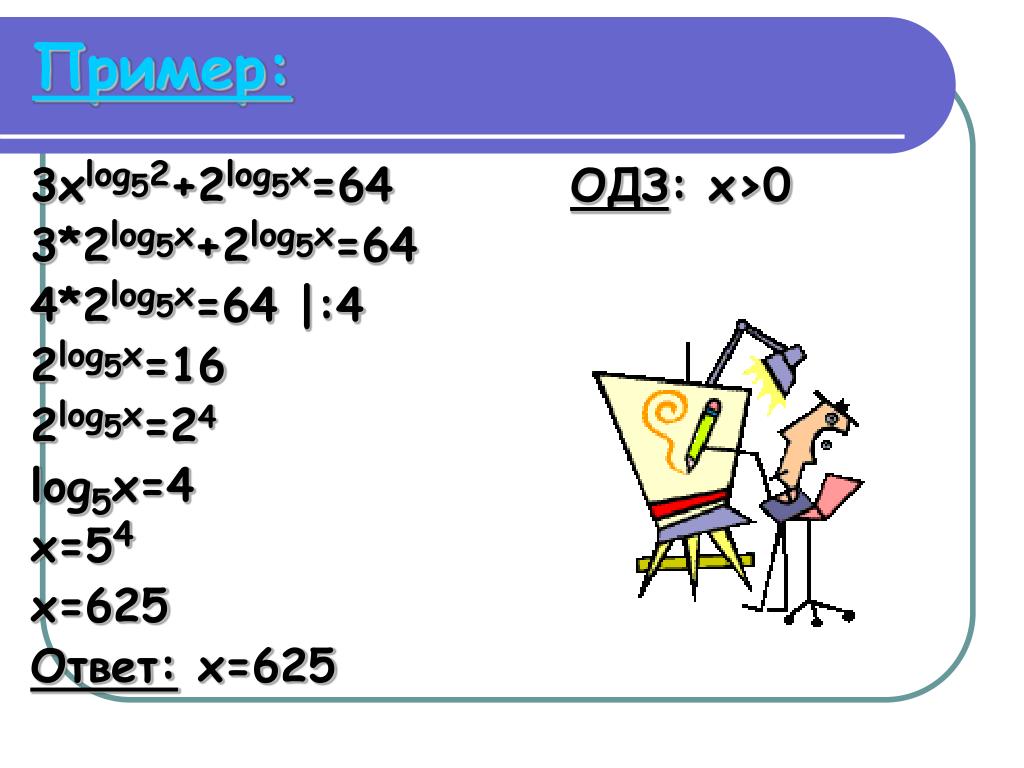
Решить логарифмическое уравнение: log_2 ( 4 x + 3 ) + log_2 ( 1 - 2 x ) = 1. Log5x=2. Log1/5x>=-1. Log3 x 5 3. Log(4x+5)=log1/3( x²+8 x) ответ.
|
Log2(-5-x)=1. Логарифмические уравнения log3(5x\2)=1. 3log3 5. Логарифмические уравнения log2/3 + log3. Log3 x 5 3.
|
Log4x>1. 2log2(x5–√)−log2(x1−x)≤log2(5x2+1x−2). Log 3 5* log 3 5. Log5(2x+3)>log5(x-1). Log1/5(5-x)=-2.
|
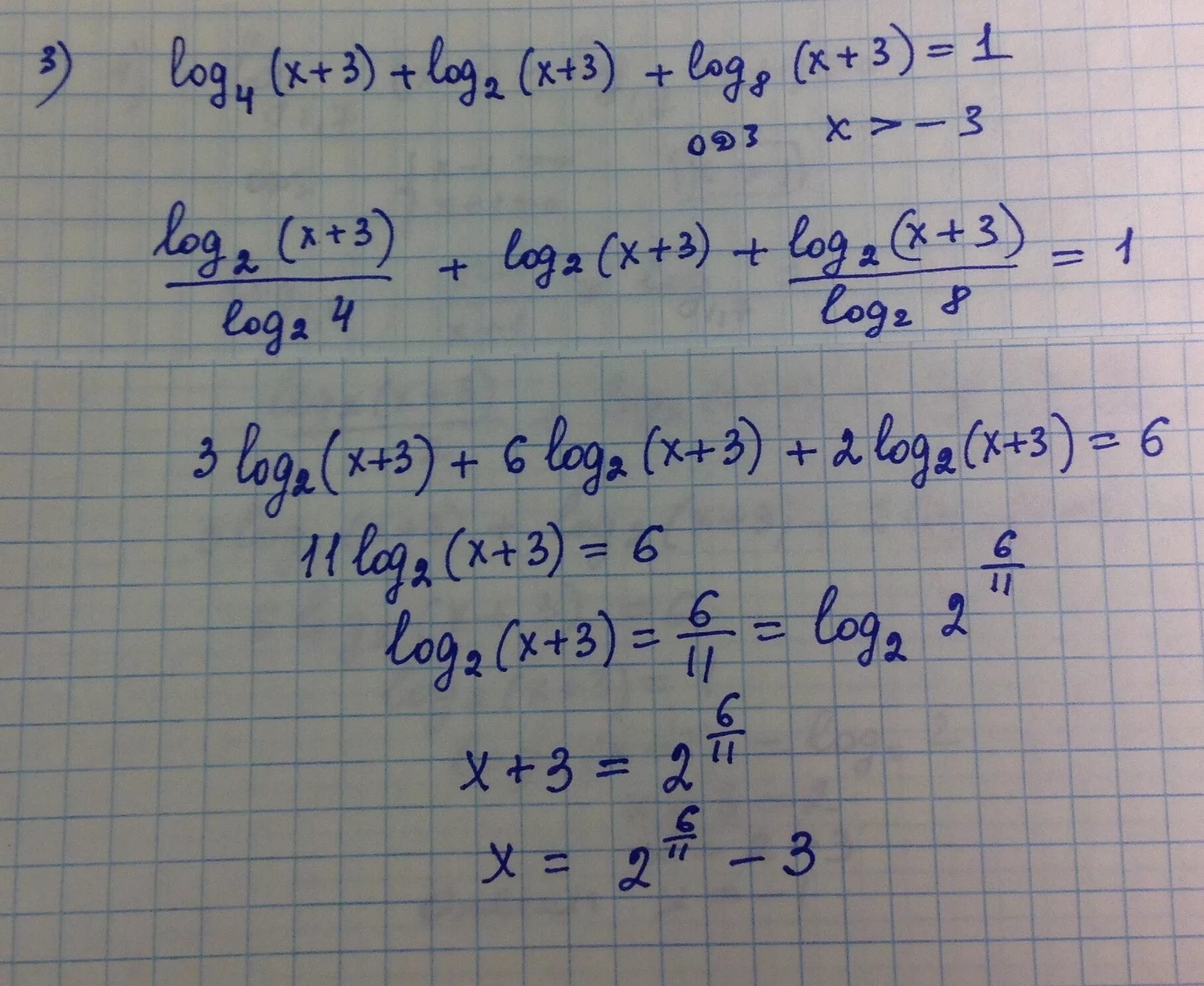Log(2) (2x 3-2x 2 -2x) =log2 (x3-2x2-2x). Log5(2x-1)=2. Log2 x 5 log2 x+2 3. Log0,5 (2х-4)=-1. Log5 7 x log5 3 x +1 одз.
|
Log2 x log2 x-3 +1 log2 x 2-3x. Log2 x 5 log2 x+2 3. Log2(х+3)=−1. Решение log 0,5 (3x-1)=-3. Log3 x 5 3.
|
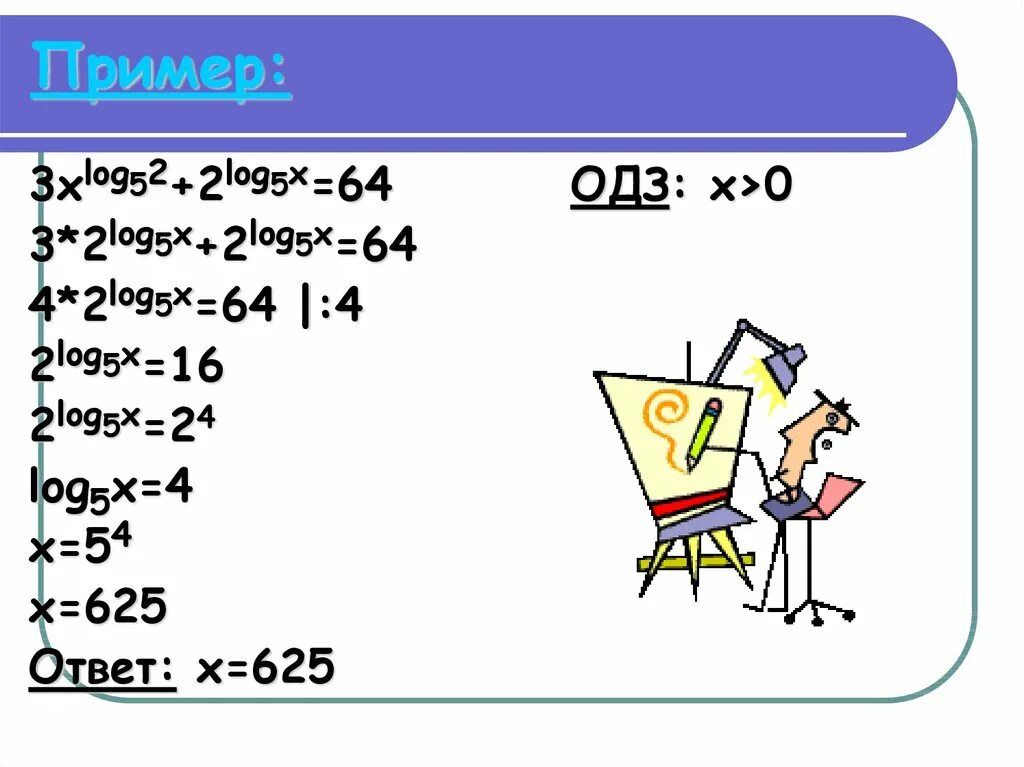Log3(2x-5)>=log3(x-3). Log2(x+2)=5. 4. Log5(2x-1)=2. Log3 x 5 3.
|
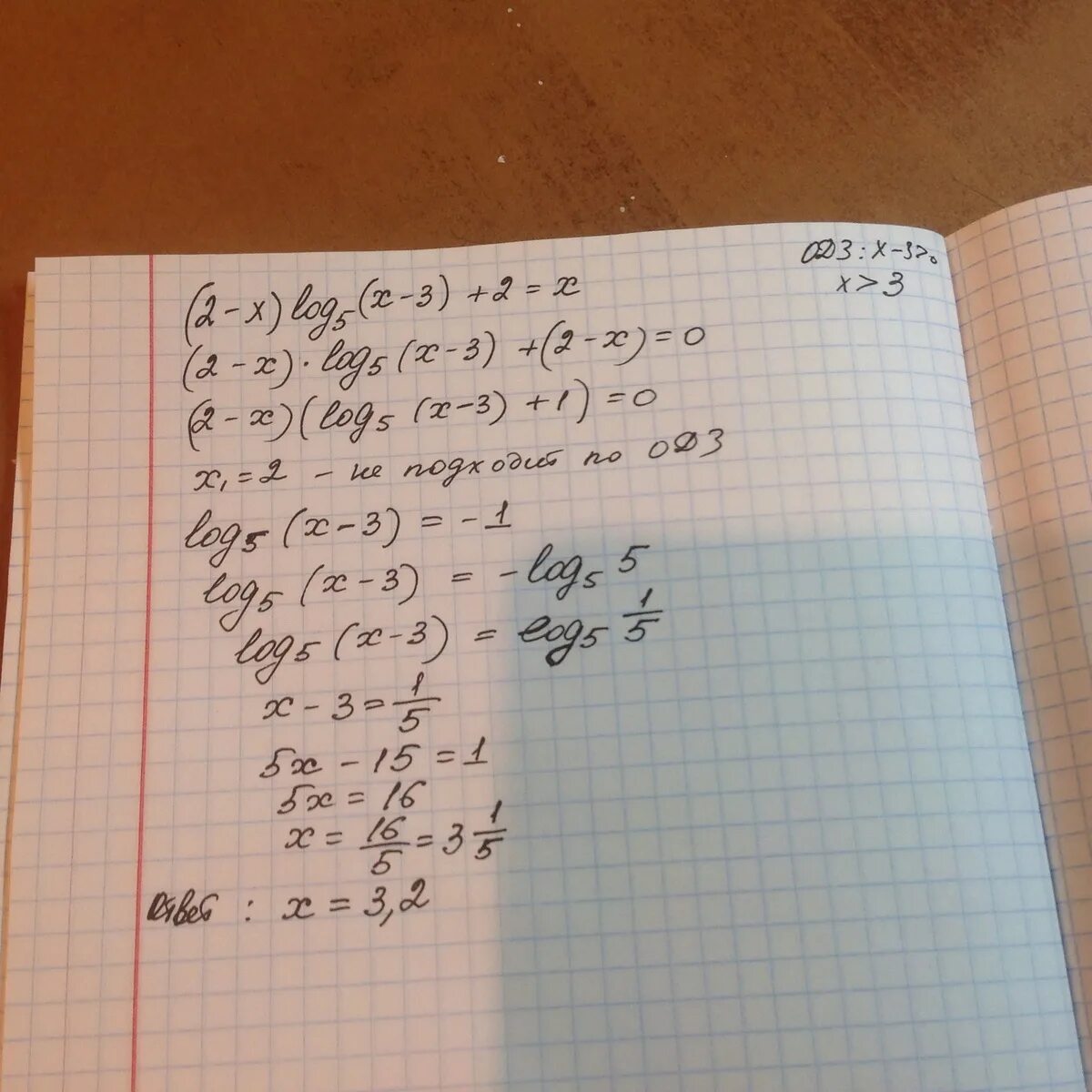Log2x<1/2. Решить неравенство log1/3 x-5 1. Log3 x 5 3. Log0 2 x 2 4 x-8 x-5. Log3 9.
|
Логарифмические уравнения log12 (x^2-x)=1. Найдите корень уравнения log3(4 - x) = 4. Log5(х^2-7х-35)=2. Log5x>1. Логарифмические уравнения log 3 (x) = x-2.
|
