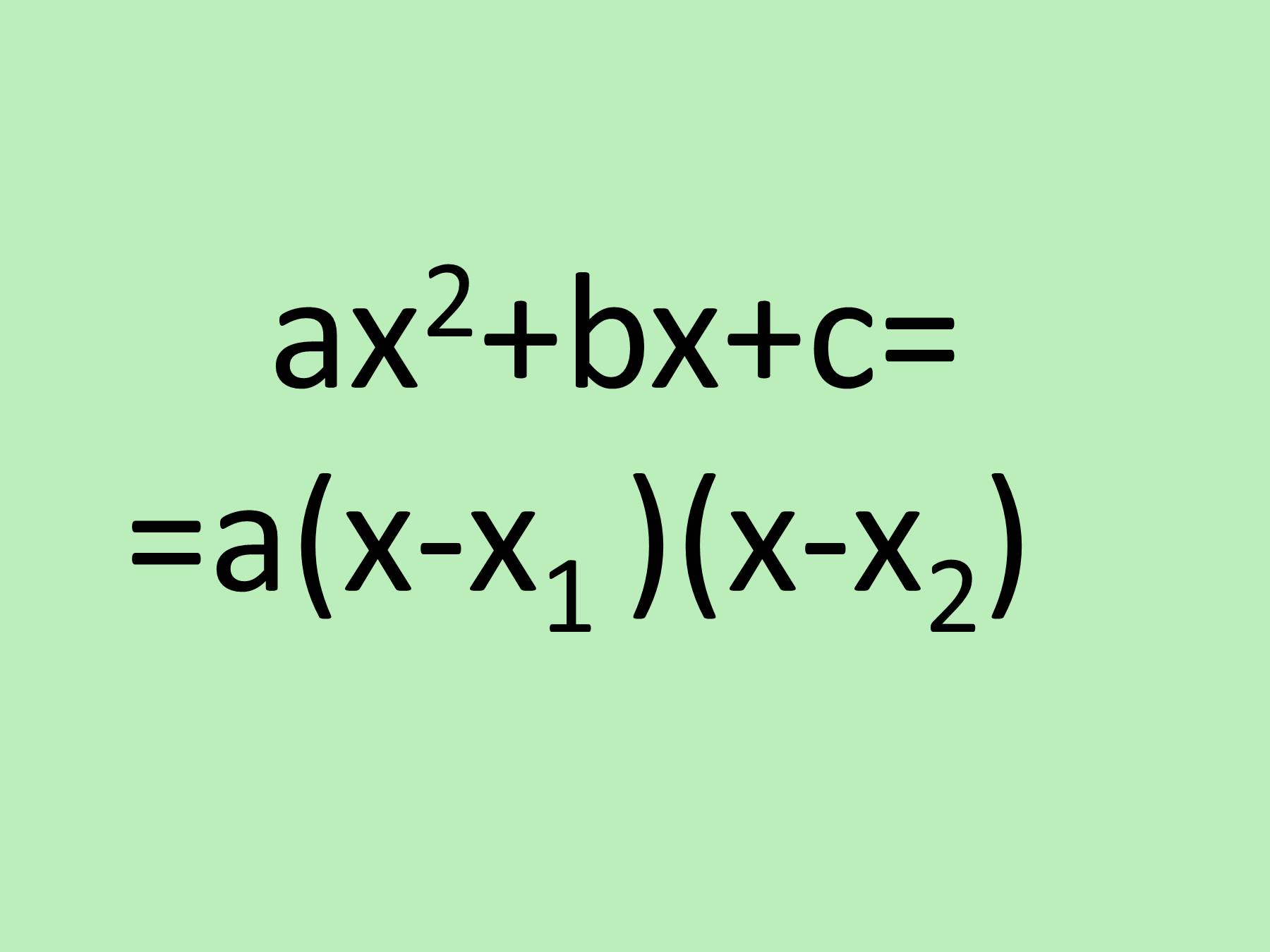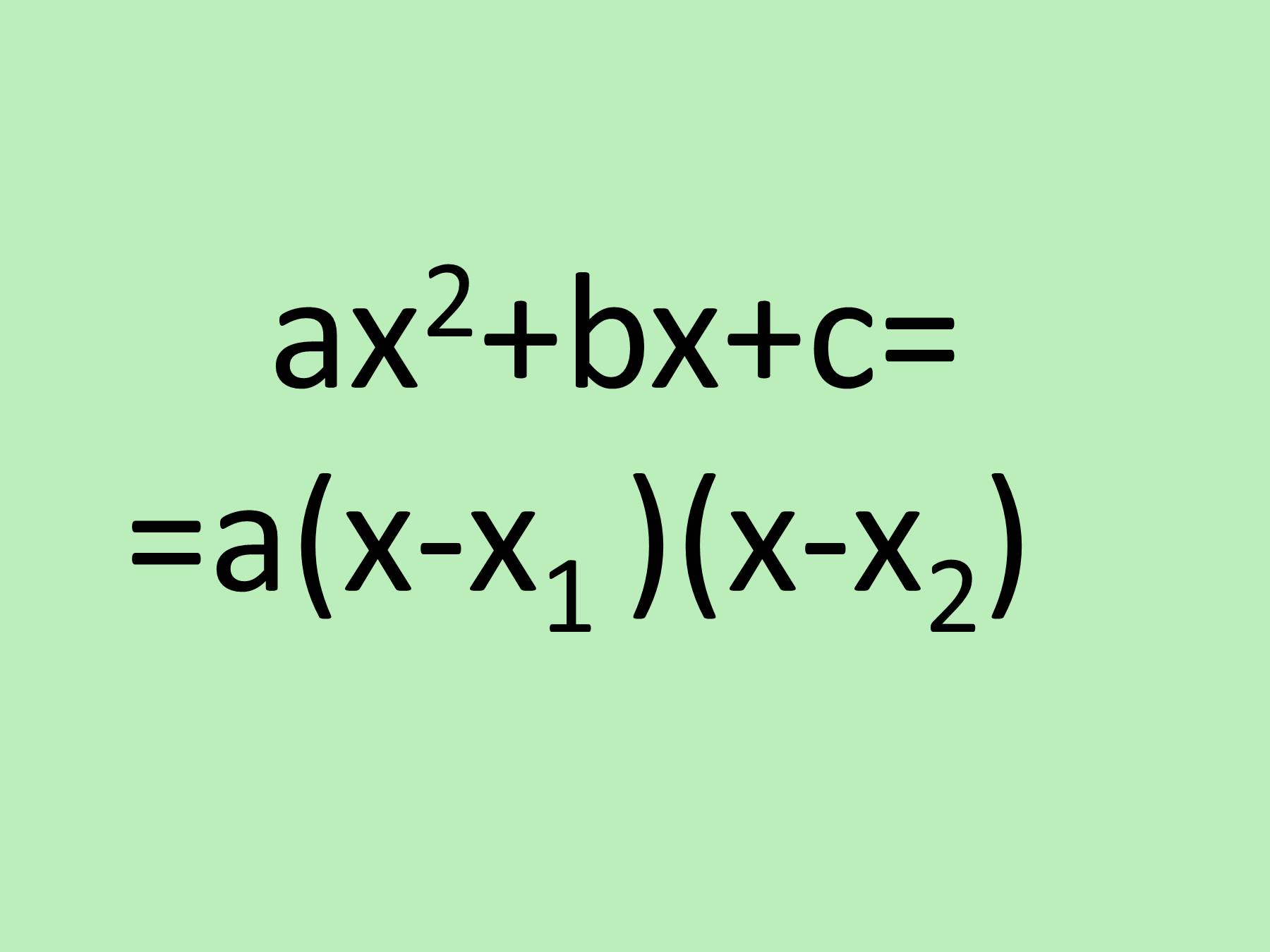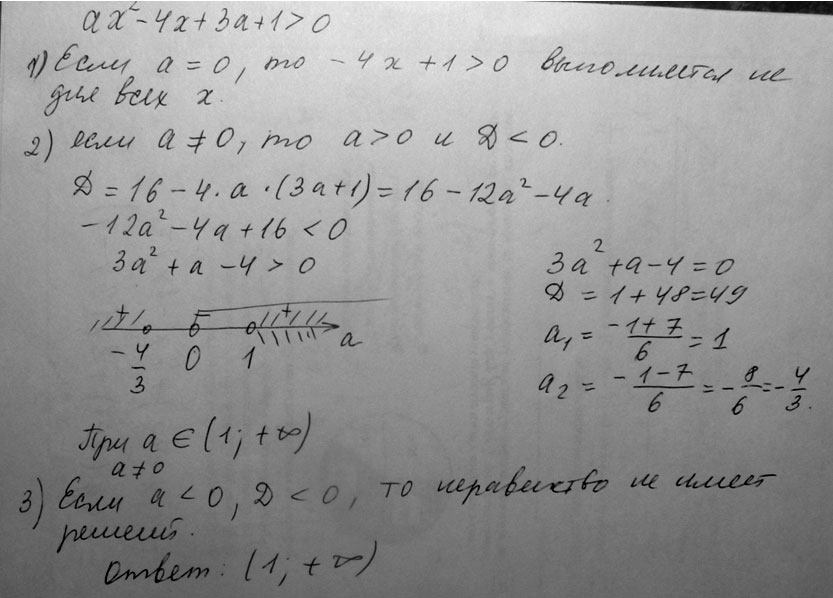Ax x2 1 ax x2. Ax x2 1 ax x2. Ax x2 1 ax x2. формула a x x1 x-x2. Yx= ax2+bx+c. Ax x2 1 ax x2. Ax x2 1 ax x2. Ax x2 1 ax x2. формула a x x1 x-x2. Yx= ax2+bx+c. |  Ax^2+b=0. Ax2 - 2x = 0. решение квадратных уравнений с параметром. Ax2+bx+c f(-12). формула квадратного трехчлена ax2+bx+c. Ax^2+b=0. Ax2 - 2x = 0. решение квадратных уравнений с параметром. Ax2+bx+c f(-12). формула квадратного трехчлена ax2+bx+c. |
 Ax2 bx c a x x1 x x2. Ax2+bx+c 0. |1-ax| = 1 + (1 - 2a)x + ax2. функция y a x m 2. функция f x ax2+bx+c. Ax2 bx c a x x1 x x2. Ax2+bx+c 0. |1-ax| = 1 + (1 - 2a)x + ax2. функция y a x m 2. функция f x ax2+bx+c. |  формула a x x1 x-x2. решение квадратных уравнений с параметром. квадратные уравнения с параметром. уравнение x2=a. Ax x2 1 ax x2. формула a x x1 x-x2. решение квадратных уравнений с параметром. квадратные уравнения с параметром. уравнение x2=a. Ax x2 1 ax x2. |
 Ax^2+x=0. Ax bx c a x-x1 x-x2. Ax2-4ax+4a. Ax x2 1 ax x2. решение уравнений x2. Ax^2+x=0. Ax bx c a x-x1 x-x2. Ax2-4ax+4a. Ax x2 1 ax x2. решение уравнений x2. |  X2 + 2ax + a2. Ax2+bx=0. решение квадратного уравнения ax2+bx+c 0. X2+4ax+1-2a+4a2 параметра. найти значение параметра а. X2 + 2ax + a2. Ax2+bx=0. решение квадратного уравнения ax2+bx+c 0. X2+4ax+1-2a+4a2 параметра. найти значение параметра а. |
 2ax+b. Y=ax-x^2. квадратичное уравнение с параметром. Ax x2 1 ax x2. правило разложения квадратного трехчлена на множители. 2ax+b. Y=ax-x^2. квадратичное уравнение с параметром. Ax x2 1 ax x2. правило разложения квадратного трехчлена на множители. |  Ax x2 1 ax x2. Ax x2 1 ax x2. Ax2-4x+c. X2-ax корень 4-4x-x 2 + 2a2. как решать уравнения ax3+bx+c 0. Ax x2 1 ax x2. Ax x2 1 ax x2. Ax2-4x+c. X2-ax корень 4-4x-x 2 + 2a2. как решать уравнения ax3+bx+c 0. |
 X2+4x-a/15x2-8ax+a2. найдите значение параметра. (1/x-1 + x + 1) : (x^2/1-2x+x^2). Ax^2+x=0. прямая является касательной к графику функции. X2+4x-a/15x2-8ax+a2. найдите значение параметра. (1/x-1 + x + 1) : (x^2/1-2x+x^2). Ax^2+x=0. прямая является касательной к графику функции. |  X2 + 2ax + a2. параметр x^2+a^2-2x-6a=|6x-2a|. Ax x2 1 ax x2. решение уравнения ax2+bx+c. Ax bx c a x-x1 x-x2. X2 + 2ax + a2. параметр x^2+a^2-2x-6a=|6x-2a|. Ax x2 1 ax x2. решение уравнения ax2+bx+c. Ax bx c a x-x1 x-x2. |
 уравнения с параметром. Ax x2 1 ax x2. F x ax2+bx+c. X2 + 2ax + a2. (ax-1)(2x^2-x-a)=0. уравнения с параметром. Ax x2 1 ax x2. F x ax2+bx+c. X2 + 2ax + a2. (ax-1)(2x^2-x-a)=0. | 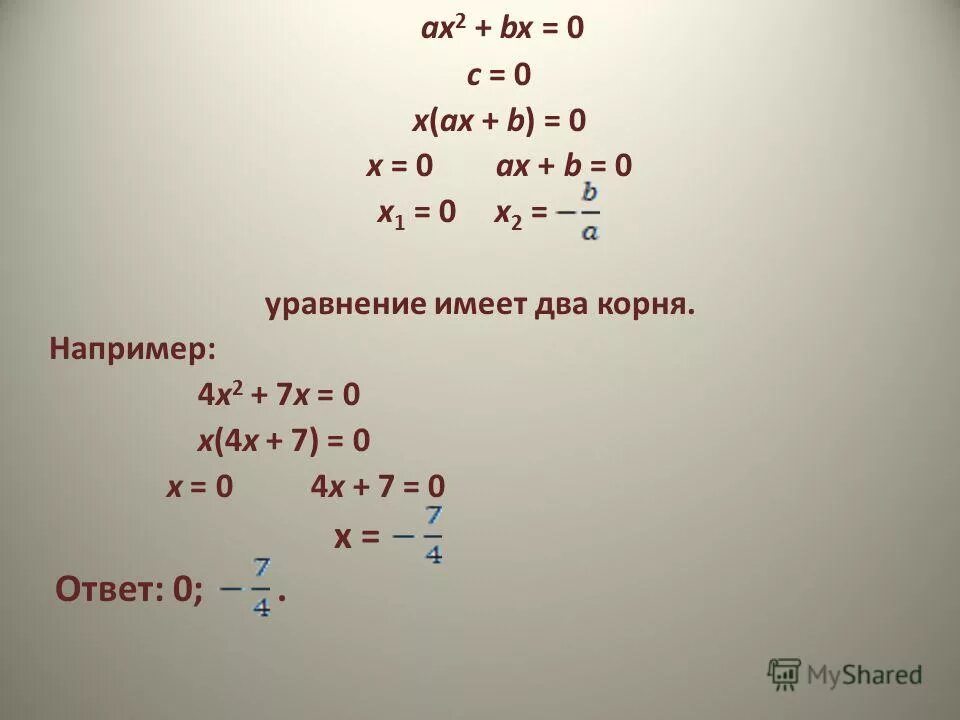 Ax x2 1 ax x2. квадратное уравнение ax2+bx. X/(a2-1)=a/(ax-1). найдите все значения параметра при котором. прямая является касательной к графику. Ax x2 1 ax x2. квадратное уравнение ax2+bx. X/(a2-1)=a/(ax-1). найдите все значения параметра при котором. прямая является касательной к графику. |
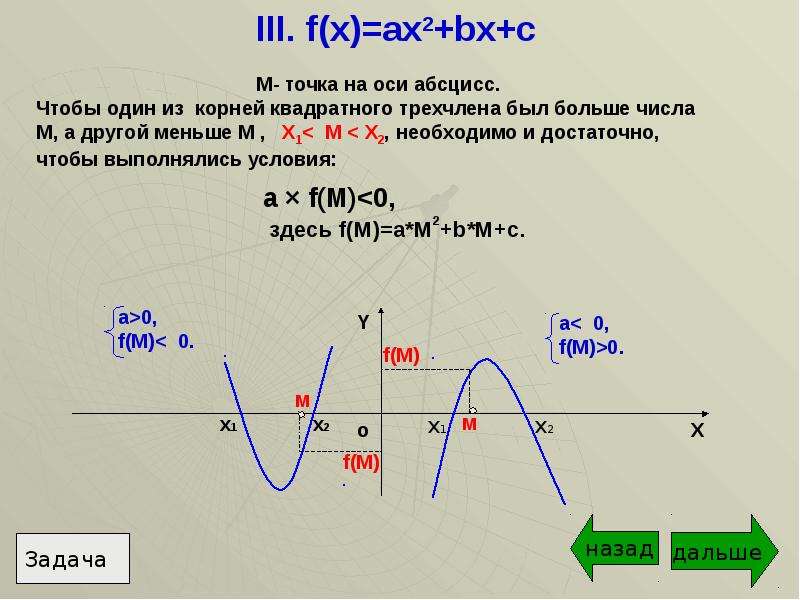
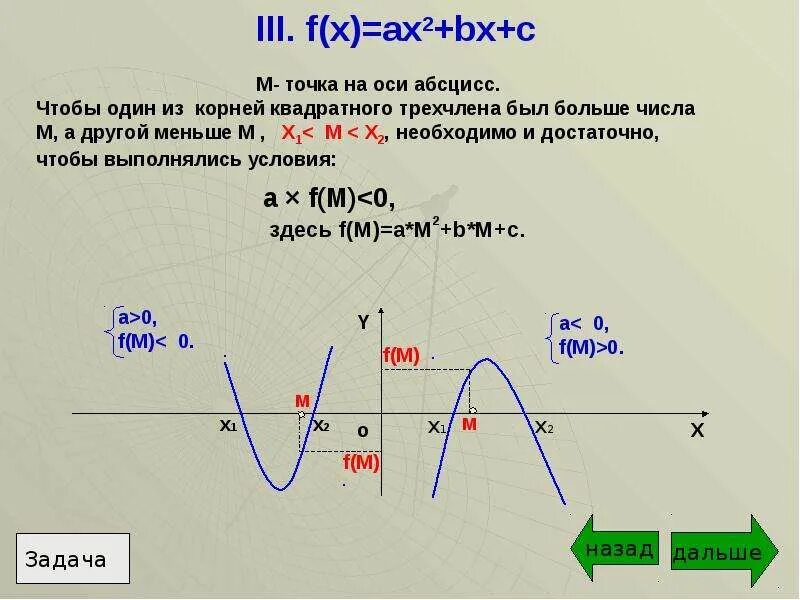 ( x-a )(ax-2a+3)>=0. F x ax2+bx+c и м – точка на оси ox. Ax x2 1 ax x2. Ax x2 1 ax x2. X2+ax+b=0. ( x-a )(ax-2a+3)>=0. F x ax2+bx+c и м – точка на оси ox. Ax x2 1 ax x2. Ax x2 1 ax x2. X2+ax+b=0. |  X2+ax+b=0. Y. Ax²+2x+1, 5a-1>0. неполные квадратные уравнения ax2+bx. F(x) = ax^2. X2+ax+b=0. Y. Ax²+2x+1, 5a-1>0. неполные квадратные уравнения ax2+bx. F(x) = ax^2. |
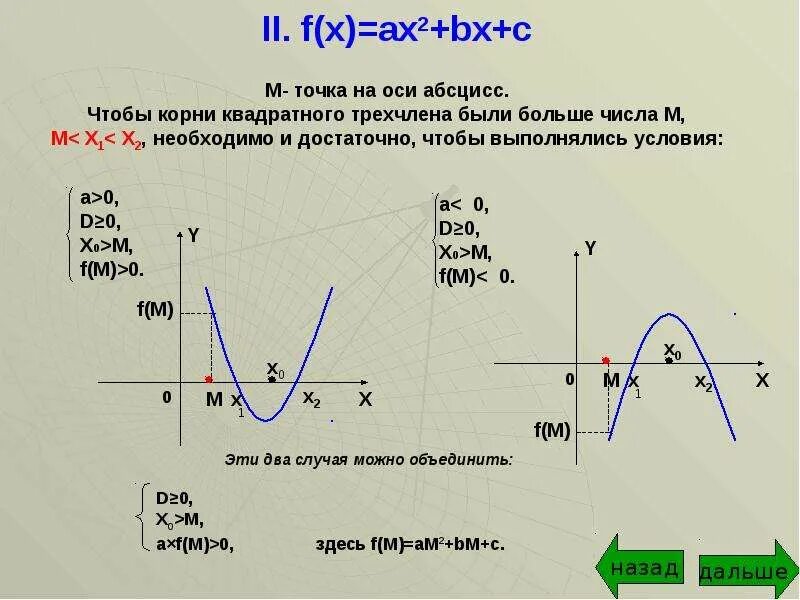 прямая является касательной к графику функции найдите с. Ax2 bx c a x x1 x x2. Ax x2 1 ax x2. уравнения с параметром. Ax x2 1 ax x2. прямая является касательной к графику функции найдите с. Ax2 bx c a x x1 x x2. Ax x2 1 ax x2. уравнения с параметром. Ax x2 1 ax x2. |  3ax(x-2a)-6ax(a-x)=. X&y. Ax x2 1 ax x2. Ax x2 1 ax x2. Ax2+bx=0. 3ax(x-2a)-6ax(a-x)=. X&y. Ax x2 1 ax x2. Ax x2 1 ax x2. Ax2+bx=0. |
 Ax x2 1 ax x2. X^2+bx+c=(x-x1)(x-x2). Ax x2 1 ax x2. Ax2+bx. Ax2=0. Ax x2 1 ax x2. X^2+bx+c=(x-x1)(x-x2). Ax x2 1 ax x2. Ax2+bx. Ax2=0. | 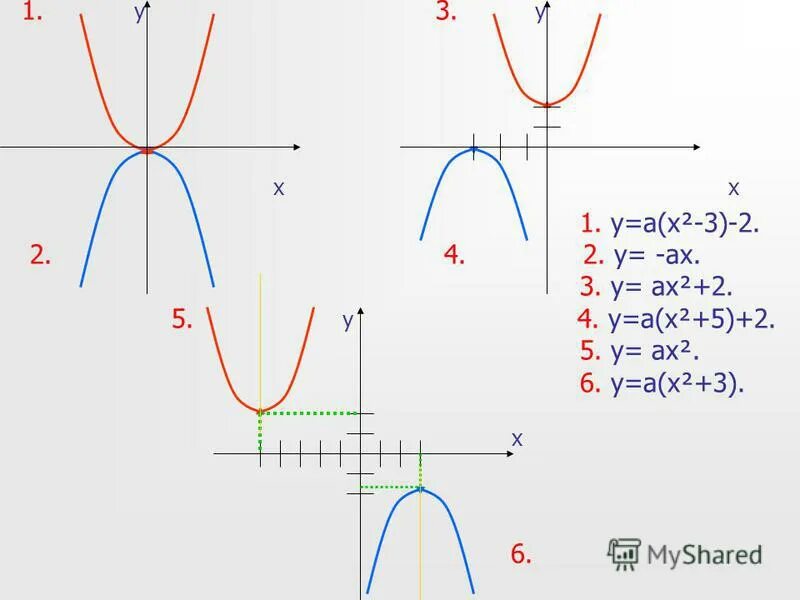 X^2=0. формула a x x1 x-x2. Ax x2 1 ax x2. F x ax2+bx+c. 2ax+b. X^2=0. формула a x x1 x-x2. Ax x2 1 ax x2. F x ax2+bx+c. 2ax+b. |
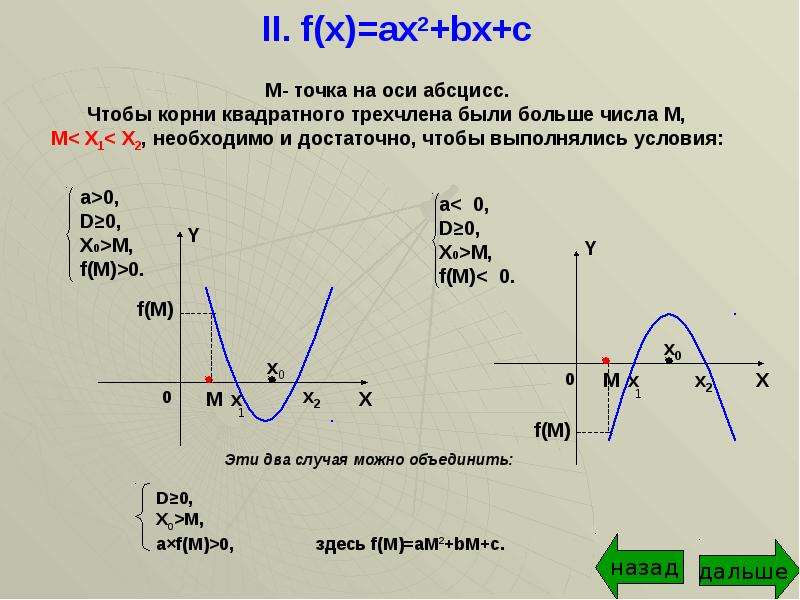
 F(x)=ax+bx+c. X2+ax+a2. Ax2 bx c a x x1 x x2. Ax^2+b=0. прямая y 3x 1 является касательной к графику функции. F(x)=ax+bx+c. X2+ax+a2. Ax2 bx c a x x1 x x2. Ax^2+b=0. прямая y 3x 1 является касательной к графику функции. | 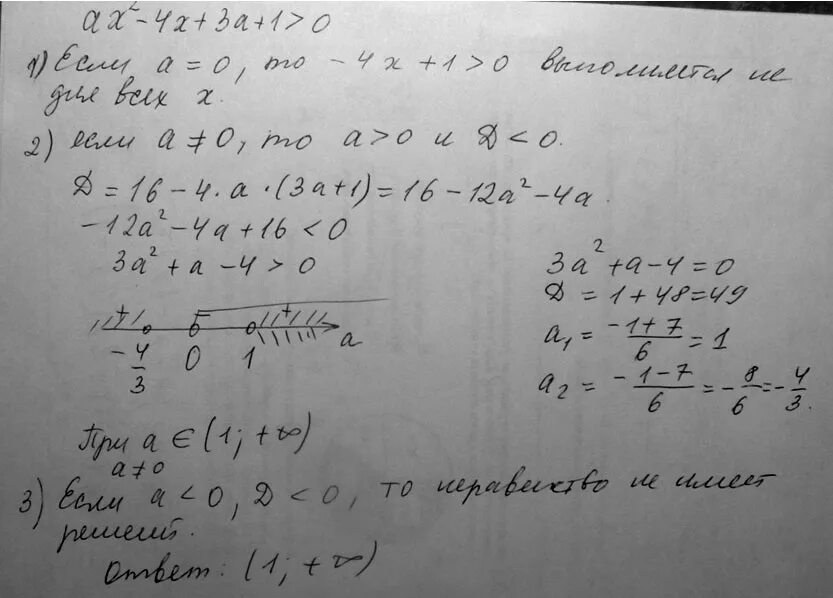 решить уравнение a^2x^2+4(a-2)x+4= 0. решить уравнение a^2x^2+4(a-2)x+4= 0. |